Skip to main content

Study Guide

Field 133: Mathematics (5–9)
Sample Multiple-Choice Questions

Expand All Answers | Collapse All Answers

The following reference material will be available to you during the test:

Subarea 1—Pedagogical Knowledge and Practices for Teaching Mathematics

Objective 001—Promote Equitable Teaching

1. A teacher displays a ratio problem and a solution to the problem that contains an error. The teacher can provide students with the greatest opportunity to share their thinking about the mathematics by taking which of the following actions?

  1. providing all students with time to identify the error and then randomly calling on someone to explain what is incorrect
  2. instructing students to write what they observe in the solution and then directing the students to share what they wrote in small groups
  3. selecting a volunteer to demonstrate how to do the problem correctly in front of the class and then encouraging students to ask questions
  4. displaying four possible descriptions of the error and then directing all students to hold up their fingers to indicate which description matches the error
Answer. Enter to expand or collapse. Answer expanded
Correct Response: B.
Objective 003—Implement Effective Instruction

2. A seventh-grade math teacher demonstrates two different methods for solving a multistep equation and asks the class to compare the strategies.

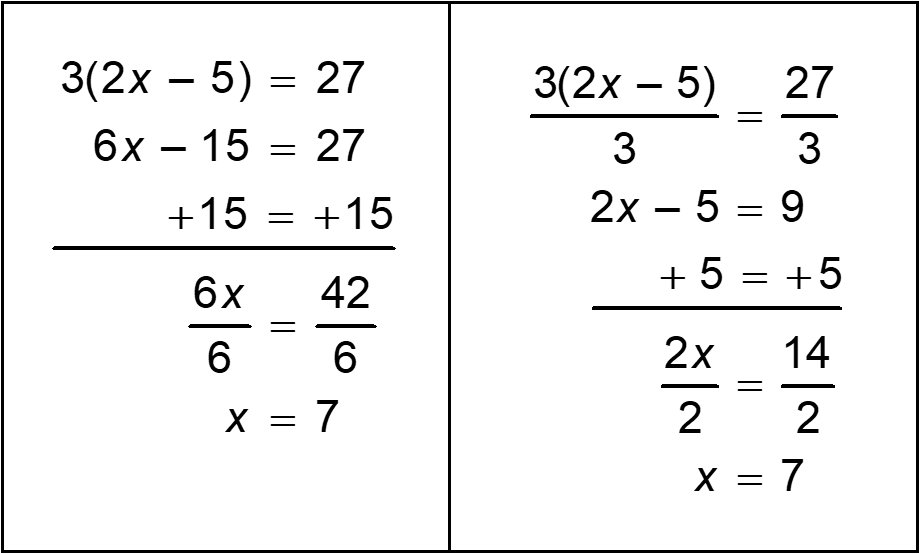
two different methods to solve a multistep equation

The equation 3 times the quantity 2 x minus 5 equals 27 is solved using two different strategies. The strategy on the left begins by distributing the factor of 3 to the quantity 2 x minus 5, and the strategy on the right begins by dividing both sides of the equation by 3. Both strategies arrive at the correct result, x equals 7.

The students agree that both methods always work, but they prefer dividing the coefficient of 3 rather than distributing it to prevent errors. Which of the following equations can the teacher assign to students to promote their reasoning regarding when using the distributive property is a more efficient strategy?

  1. 4 times the quantity 4 minus x equals 40
  2. 3 times the quantity 5 x minus 9 equals 18
  3. 3 times the quantity 4 x plus 1 equals 35
  4. negative 1 plus 4 times the quantity 2 x minus 7 equals 23
Answer. Enter to expand or collapse. Answer expanded
Correct Response: C.
Objective 004—Enhance Teaching Through Collaboration with Colleagues, Families, and Community

3. A group of middle school math teachers meets once a week to discuss strategies that they can use to promote their students' success with mathematics. In one meeting, the teachers work to identify instructional strategies for helping students make connections between mathematics and everyday life. Discussing which of the following questions should be the group's highest priority?

  1. What are good examples of real-world connections that students make to math concepts?
  2. Which topics in the mathematics curriculum allow students to form connections to real life?
  3. What types of question structures maximize opportunities for students to engage in productive discourse?
  4. In what ways does the existing mathematics curriculum prevent students from forming connections to real life?
Answer. Enter to expand or collapse. Answer expanded
Correct Response: A.

Subarea 2—Students as Learners of Mathematics

Objective 005—Anticipate and Attend to Students' Thinking About Mathematics Content

4. A teacher assigns an exit slip following an introductory lesson on the definition of a function. One student response is shown.

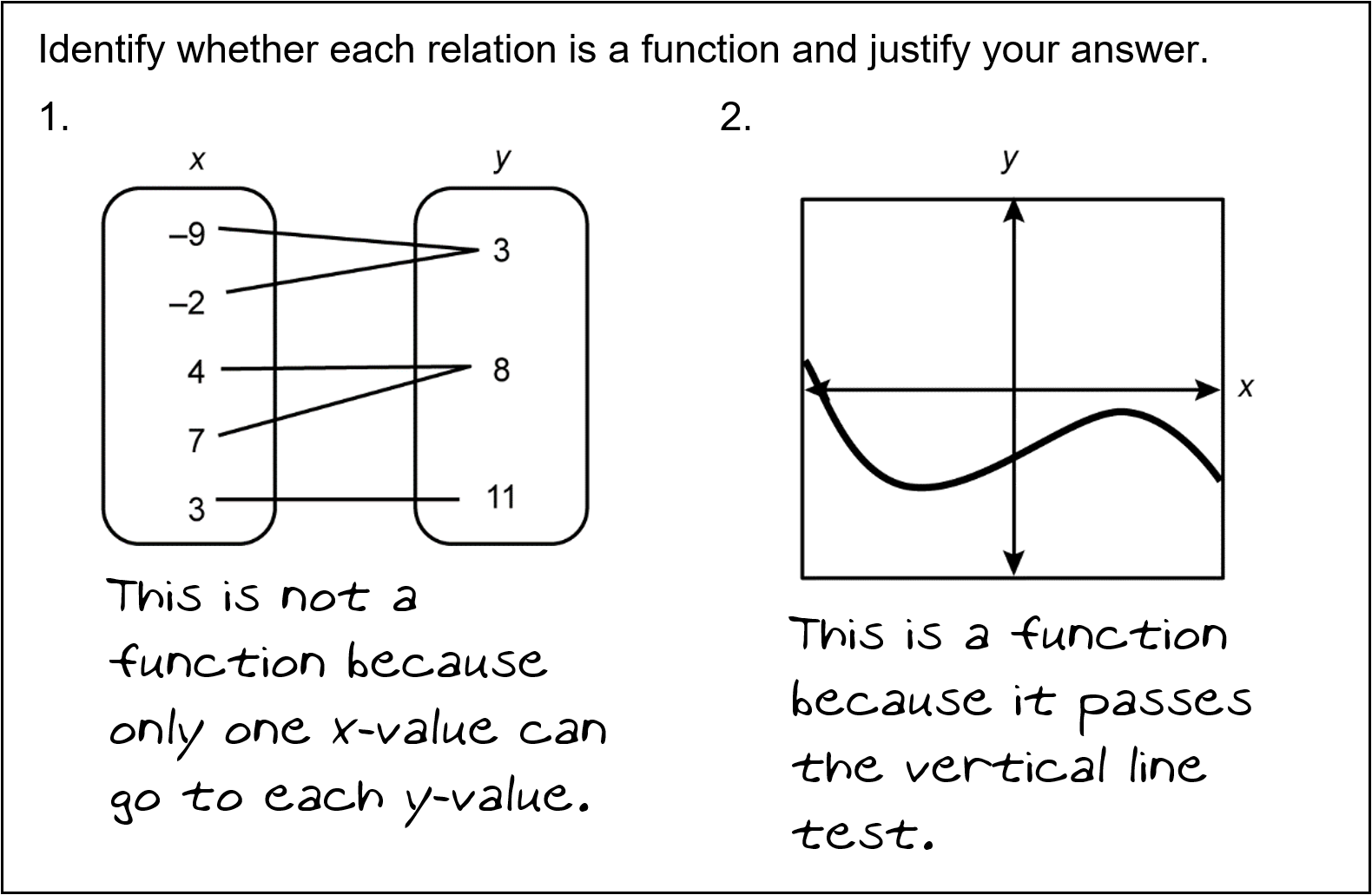
an exit slip on the definition of a function

An exit slip has the following instructions: Identify whether each relation is a function and justify your answer.

The first problem shows a mapping diagram with a domain of negative 9, negative 2, 4, 7, and 3 and a range of 3, 8, and 11. The negative 9 and negative 2 from the domain are mapped to 3 in the range. 4 and 7 from the domain are mapped to 8 in the range. And 3 in the domain is mapped to 11 in the range. The student's response reads, "This is not a function because only one x value can go to each y value."

Problem number 2 shows the graph of a polynomial function. The student response says, "This is a function because it passes the vertical line test."

Which of the following analyses of the student's level of understanding is most accurate?

  1. The student can correctly identify functions from discrete points, but they exhibit misconceptions about how to apply the vertical line test.
  2. The student exhibits misconceptions about the definition of a function, but they can procedurally apply the vertical line test to identify functions.
  3. The student exhibits the misconception that every function must be one-to-one, and they consistently apply that logic when using the vertical line test.
  4. The student exhibits a misconception about the domain and range of a function, and they consistently apply that logic when using the vertical line test.
Answer. Enter to expand or collapse. Answer expanded
Correct Response: B.
Objective 006—Promote Students' Engagement in Mathematical Practices

5. An eighth-grade student discusses the following system of linear equations with their teacher.

X minus 2 y equals 10
Y equals 1 half x minus 3

Student: I want to check the slopes of each equation before I do anything else, but I only see a slope in the second equation. So, what do I do now?

Which of the following questions can the teacher use to best support the student's comparison of the slopes of these lines?

  1. "How many times bigger is the coefficient of x in the first equation than in the second equation?"
  2. "What observations can we make if we solve an equation of the form A X plus B Y equals C for y?"
  3. "What can you discover about the value of x if we substitute 0 for y in the first equation?"
  4. "How does dividing both sides by 2 change the coefficient of x in the first equation?"
Answer. Enter to expand or collapse. Answer expanded
Correct Response: B.
Objective 007—Cultivate Positive Mathematical Identities of Students

6. Eighth-grade students work in structured groups of three to solve multistep equations on a whiteboard. The teacher structured the groups to promote discussion by assigning each group member a specific role to play in a conversation about the problem, and the students rotate through all the roles as they work. The student participating in the role of "the skeptic" asks questions about justifying the work, such as "How do you know that step is correct?" and "Why does it make sense to use multiplication like that?" This approach counters negative beliefs about who is good at mathematics in which of the following ways?

  1. It assures the students that incorrect work will not be penalized.
  2. It reduces the risk that students will make mistakes with their work.
  3. It encourages the students to use correct vocabulary when discussing their work.
  4. It demonstrates that students of all levels of understanding are expected to ask questions.
Answer. Enter to expand or collapse. Answer expanded
Correct Response: D.

Subarea 3—Understanding of Social Contexts of Mathematics Teaching and Learning

Objective 008—Provide Access and Opportunity

7. Seventh-grade math students are placed into either a standard math course or an advanced math course for the following year. The advanced course integrates technological applications into the mathematics of the curriculum. In which of the following ways does this system increase inequity in learning mathematics?

  1. The system limits opportunities for students in the standard math course to become familiar with technological applications in mathematics.
  2. The integration of technology into the advanced class reduces the time students have for processing specific mathematical concepts.
  3. Students enrolled in the standard math course will not get the necessary technological and mathematics support they need.
  4. This system increases the likelihood that students become dependent on technological applications for mathematical tasks.
Answer. Enter to expand or collapse. Answer expanded
Correct Response: A.
Objective 009—Understand Power and Privilege in the History of Mathematics Education

8. A seventh-grade math teacher develops a learning activity early in a unit on simple and compound probability. In this lesson, groups of students will determine the likelihood of selecting a specific set of playing cards from a standard deck (e.g., drawing a 3, drawing two red cards in a row, drawing a 5 of diamonds). The teacher can best support equitable learning opportunities in this lesson by taking which of the following actions?

  1. assigning values of 11, 12, and 13 to the face cards (i.e., Jack, Queen, and King) and referencing these point values throughout the activity
  2. ensuring that students understand how to determine the probability of selecting a single card before moving on to combinations of cards
  3. allowing each group of students opportunities to determine the probabilities of outcomes that they choose
  4. providing each group of students with a deck of cards to use during the activity
Answer. Enter to expand or collapse. Answer expanded
Correct Response: D.
Objective 010—Enact Ethical Practices for Advocacy

9. A group of ninth-grade algebra teachers invites students who are English learners at the developing level of proficiency to several lunch sessions. The teachers intend to use these lunch sessions to better understand their students' ability to comprehend lesson content. Which of the following conversations is best suited for this purpose?

  1. learning about interests that students have outside of the mathematics classroom
  2. asking students about their experiences participating in mathematical learning activities
  3. having students describe whether the amount of work they receive in class is appropriate
  4. discussing whether students have effective routines for studying and completing homework
Answer. Enter to expand or collapse. Answer expanded
Correct Response: B.

Subarea 4—Know Relevant Mathematical Content

Objective 011—Understand Essential Concepts in Number

10. An eighth-grade math teacher concludes a lesson on classifying numbers within the real number system. The teacher assigns an exit slip and instructs students to draw a Venn diagram to illustrate one fact from the lesson. Which of the following student diagrams best demonstrates understanding of the real number system?

  1. A small circle, labeled negative numbers, is completely nested within a larger circle, labeled integers.
  2. A circle labeled whole numbers partially overlaps another circle. The intersection of the two circles is labeled rational numbers.
  3. Two circles are shown that do not overlap. One circle is labeled whole numbers, and the other circle is labeled integers.
  4. A small circle, labeled integers, is completely nested within a larger circle, labeled rational numbers.
Answer. Enter to expand or collapse. Answer expanded
Correct Response: D.
Objective 012—Understand Essential Concepts in Ratios and Proportional Relationships

11. A seventh-grade math teacher observes a student solve the following problem.

an exit slip on the definition of a function

A word problem is shown. The word problem reads: A video costs 12 dollars and 50 cents before tax. The sales tax is 6 percent. What is the total cost of the video in dollars?

Below the word problem, a student's solution shows the following: the proportion x divided by 12.50 equals 106 divided by 100 is shown. The second step shows the equation 1325 equals 100 x with both sides divided by 100. The hundreds on the right are crossed out and the final equation is 13.25 equals x.

Teacher: Can you explain why you used 106 in your proportion?

Student: I saw someone do it online that way. You add 100 to the tax to get the number in the proportion, but I don't know why.

Which of the following responses can the teacher use to describe this solution method most effectively?

  1. "This method works because you are essentially multiplying the cost of the video by 1.06."
  2. "If you use just a 6 instead of the 106 in your proportion, your final answer is the amount you pay in sales tax."
  3. "100% of the pre-tax cost of the video is $12.50. We need an additional 6% for sales tax, so the total is 106% of the cost."
  4. "Adding 100 to the sales tax percent is a way to shorten the amount of work. This combines two steps into a single proportion."
Answer. Enter to expand or collapse. Answer expanded
Correct Response: C.
Objective 013—Understand Essential Concepts in Algebra at a Comprehensive, Robust Level

12. A student rewrites a given equation as shown.

a table depicting an equation and a student's rewriting of the equation
Original Equation Y equals 2 x squared plus 4 x minus 1
Rewritten Equation Y equals 2 times the quantity x plus 1 squared minus 3

Which of the following reasons most likely explains the student's choice to rewrite the equation in this manner?

  1. The student wants to graph the equation by creating a table of values.
  2. The student wants to locate the zeros of the graph of the function by factoring.
  3. The student plans to graph the equation using transformations of the equation Y equals x squared.
  4. The student plans to use the quadratic formula to find the zeros of the graph of the equation.
Answer. Enter to expand or collapse. Answer expanded
Correct Response: C.
Objective 014—Understand Essential Concepts in Functions (e.g., Linear, Exponential, Polynomial, Absolute Value, Piecewise-Defined)

13. At the end of a lesson on graphing quadratic functions, a teacher has students consider a quadratic function that has a vertex at the point 4, negative 3. The teacher then instructs students to complete an exit slip in which they list two other attributes that must be true of the function. Which of the following student responses is accurate?

  1. "The function does not have any x-intercepts."
  2. "The function has a domain of all real numbers."
  3. "The function is symmetrical across the line y equals 4."
  4. "The function has an absolute maximum at the point 4, negative 3."
Answer. Enter to expand or collapse. Answer expanded
Correct Response: B.
Objective 015—Understand Essential Concepts in Statistics and Probability

14. A sixth-grade teacher facilitates a lesson about the mean and median of data sets. One student says, "The median and the mean are close to being the same in all of these data sets. Why do we use both if they are so close to being the same number?" The teacher can most effectively respond to the student's question by comparing the median and mean for a data set that:

  1. has positive and negative values.
  2. contains only unique values.
  3. contains an outlier.
  4. is symmetrical.
Answer. Enter to expand or collapse. Answer expanded
Correct Response: C.
Objective 017—Understand Essential Concepts in Calculus at a Foundational, Basic Level

15. A calculus teacher shows a graph of a function that is intersected by line segments that are arranged in a stair-step pattern.

a graph of a function that is intersected by line segments that are arranged in a stair-step pattern

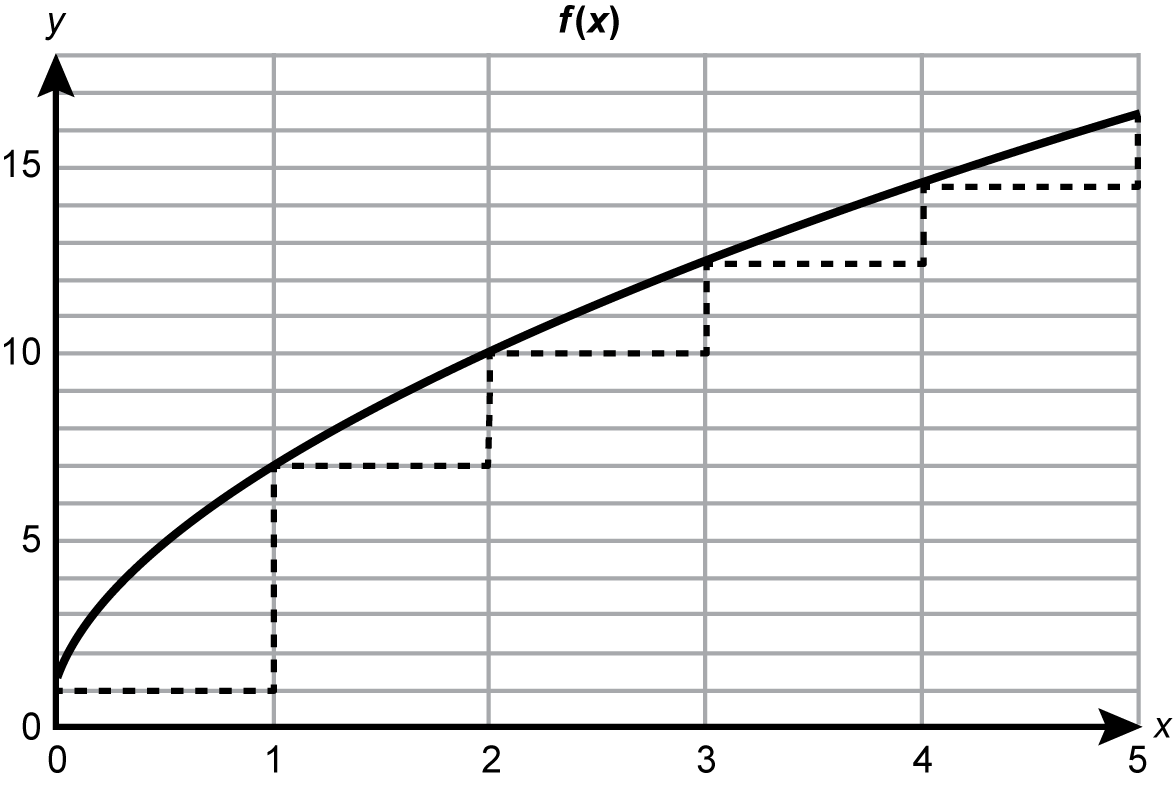
The graph of a square root function with a positive leading coefficient and a y intercept of 1 is shown in the first quadrant of the coordinate plane. A dashed horizontal line segment extends to the right from the y intercept by one unit., and then a dashed vertical line segment extends from that location to a point on the graph. Another dashed line segment extends horizontally one unit from that point on the graph, followed by another dashed vertical line extending to a point on the graph. The process repeats until there are 5 regions bounded by the graph and the dashed lines.

This graph could be used to support students' understanding of which of the following mathematical concepts?

  1. describing the instantaneous rate of change of f of x for different values of x
  2. describing how the average rate of change for a function varies over different intervals
  3. applying the concept of similar triangles to describe the average rate of change of a function
  4. creating a linear equation that can be used to approximate f of x in the interval from x = 0 to x = 5
Answer. Enter to expand or collapse. Answer expanded
Correct Response: B.
Objective 018—Understand Essential Concepts in Discrete Mathematics at a Foundational, Basic Level

16. A seventh-grade math teacher intends to use the following problem in a lesson about compound probability.

A person has 4 different pairs of pants, 6 different shirts, and 3 pairs of shoes. How many different outfits (pants, shirt, and shoes) can the person make?

The teacher can help students solve the problem efficiently by introducing which of the following discrete mathematics strategies?

  1. computing a combination
  2. drawing a complete tree diagram
  3. applying the fundamental counting principle
  4. creating an organized list of different outcomes
Answer. Enter to expand or collapse. Answer expanded
Correct Response: C.

Subarea 5—Mathematics Practices, Dispositions, Curriculum

Objective 019—Demonstrate Mathematical Practices

17. An eighth-grade math teacher provides students with scientific calculators and assigns the following problem. The teacher plans to use the problem to facilitate a discussion about the mathematical practice of attending to precision.

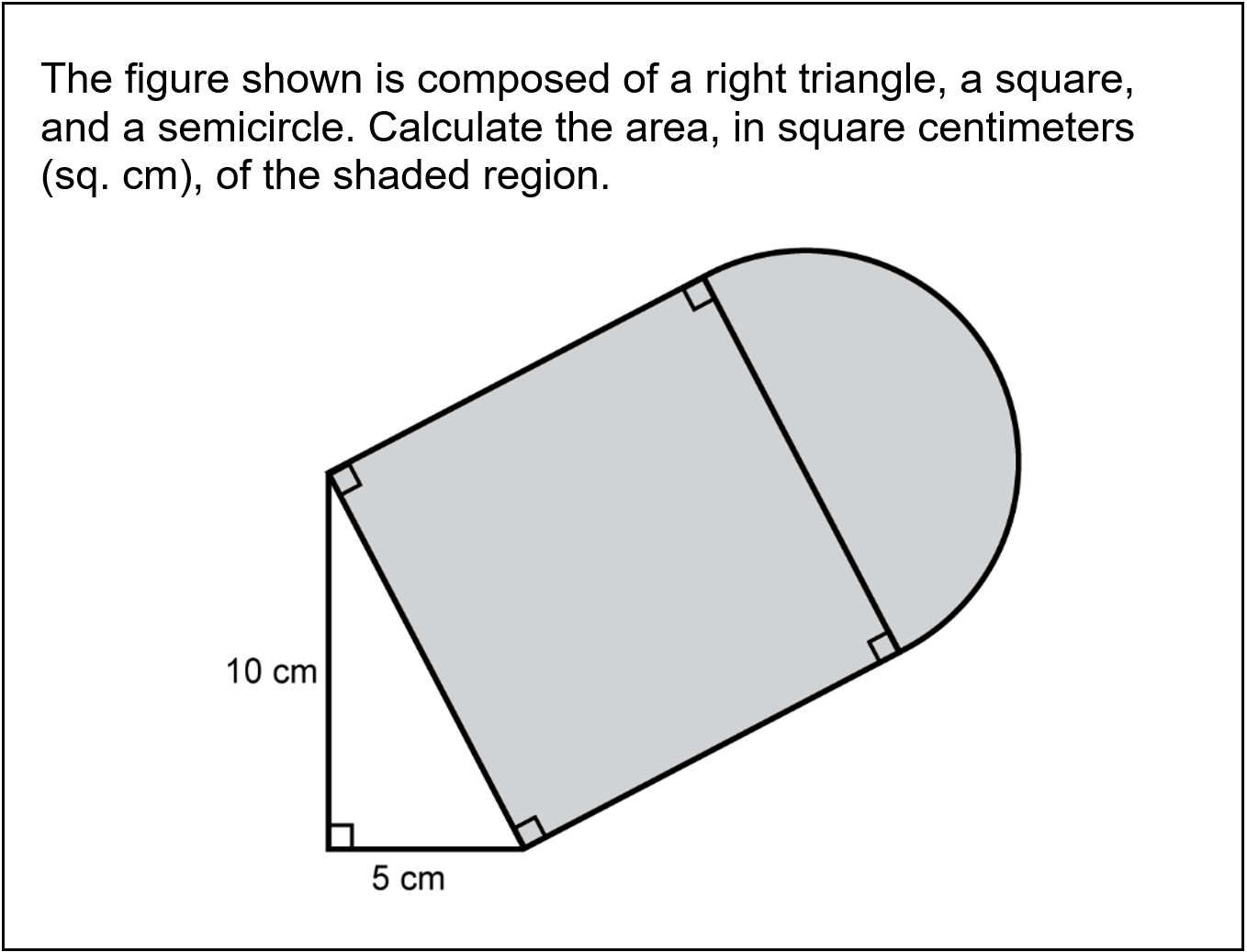
an image of a problem assigned by a math teacher

A problem is shown. The text reads: The figure shown is composed of a right triangle, a square, and a semicircle. Calculate the area, in square centimeters (sq. cm), of the shaded region.

A composite shape is shown as follows: An unshaded right triangle is shown with legs measuring 5 centimeters and 10 centimeters. The hypotenuse of the triangle forms one side of a square that is shaded. One side of the square forms the diameter of a semicircle that is also shaded.

Which of the following aspects of this problem makes it most effective for this purpose?

  1. Students must understand how the formula for the area of a circle must be adapted to calculate the area of this shape.
  2. Students must determine whether to include the area of the right triangle when calculating the area of the composite shape.
  3. The calculation involves irrational numbers, so rounding at different stages of the problem can cause variation in the final answers.
  4. The calculation involves adding the area of two shapes together, and students may misinterpret how adding two areas affects the units in the final answer.
Answer. Enter to expand or collapse. Answer expanded
Correct Response: C.
Objective 020—Exhibit Productive Mathematical Dispositions

18. During a presentation at an open house, a newly hired math teacher tells parents/guardians, "I don't think of my students in terms of their race or ethnicity when it comes to my teaching." Which of the following inequitable learning outcomes is most closely associated with the perspective the teacher expresses?

  1. ineffective classroom management
  2. a lack of responsiveness to students' individual differences
  3. lesson plans that do not provide differentiated learning strategies
  4. a classroom culture that underemphasizes the value of academic discourse
Answer. Enter to expand or collapse. Answer expanded
Correct Response: B.
Objective 021—Analyze the Mathematical Content of Curriculum

19. Students complete a graded assignment following a lesson on how to convert numbers between standard form and scientific notation. After reviewing students' work, the teacher determines that about 50% of the students demonstrate proficiency with this skill. Another 40% of the students use an incorrect exponent when converting numbers from standard form into scientific notation. Which of the following learning objectives best meets the needs of both students who are ready for new material and students who require additional support on the previous topic?

  1. how to add a number in standard form to a number written in scientific notation
  2. how to identify the relationship between place value and different powers of 10
  3. how to express numbers with scientific notation when given their standard form
  4. how to add two numbers written in scientific notation when their exponents differ
Answer. Enter to expand or collapse. Answer expanded
Correct Response: A.
Objective 022—Use Mathematical Tools and Technology

20. An eighth-grade math teacher plans a lesson about the variability of a data set. As part of this lesson, students explore how to interpret the interquartile range of a data set. The teacher uses spreadsheet software to analyze data and create representations of data sets. The teacher can best help students understand the interquartile range of a data set by using the spreadsheet software in which of the following ways?

  1. displaying a box plot of the data
  2. displaying the data on a line graph
  3. sorting data in the set by their values
  4. using a formula to convert the data values into standard scores
Answer. Enter to expand or collapse. Answer expanded
Correct Response: A.

Multiple-Subarea Passage

Use the information to answer the two questions that follow.

An eighth-grade math teacher prepares a lesson relating the distance formula to the Pythagorean theorem during a unit on coordinate geometry. The teacher will present the following diagram to the class and then use it to discuss the equation for finding the distance between two points in the coordinate plane.

an image of a diagram presented by a math teacher

Two points, x 1, y 1 and x 2, y 2, are graphed in the first quadrant of the coordinate plane. A line segment, labeled d, is shown connecting the two points. The locations of x 1 and x 2 are marked on the x axis, and the locations of y 1 and y 2 are marked on the y axis. A horizontal line extends to the right from x 1 y 1, and a vertical line extends down from x 2 y 2 to create a right triangle with side d as the hypotenuse.

Objective 002—Plan for Effective Instruction

21. Following a discussion about this diagram, students will find the distance between the points 1, negative 2 and 5, 9. Which of the following mathematical procedures would be most appropriate to review with eighth-grade students before they begin this task?

  1. separating the radical product radical ab as radical a times radical b
  2. determining the x- and y-values of a coordinate pair
  3. identifying horizontal and vertical distances between points
  4. expanding binomial expressions such as the quantity a minus b squared and the quantity a plus b squared
Answer. Enter to expand or collapse. Answer expanded
Correct Response: C.
Objective 016—Understand Essential Concepts in Geometry, Trigonometry, and Measurement

22. Which of the following equations should the teacher share with students to help them accurately connect the concept of distance in the coordinate plane to the Pythagorean theorem?

  1. x squared plus y squared equals d squared
  2. d squared minus x squared equals y squared
  3. the quantity x 2 minus x 1 squared plus the quantity y 2 minus y 1 squared equals d squared
  4. the quantity x 2 plus x 1 squared minus 2 times the quantity x 1 x 2 plus y1 y2 plus the quantity y 2 plus y 1 squared equals d squared
Answer. Enter to expand or collapse. Answer expanded
Correct Response: C.